If you are running a large public web applications like shopping and emails portals, you have handle lots of unwanted data rows for example spam emails and unused shopping cart data. Sure it will created problem in database overload. So that I want to explain a simple tip called how to use MySQL event scheduler for deleting unwanted data rows from database.
Author
Arun Kumar Sekar
Engineer, Plugin Expert
Chennai, INDIA
Engineer, Plugin Expert
Chennai, INDIA
Database
Sample database cart table contains four columns cart_id, user_id, product_id and created_at.
CREATE TABLE cart
(
cart_id INT AUTO_INCREMENT,
user_id INT,
product_id INT,
created_at TIMESTAMP DEFAULT CURRENT_TIMESTAMP ON UPDATE CURRENT_TIMESTAMP,
PRIMARY KEY (cart_id)
) ;
(
cart_id INT AUTO_INCREMENT,
user_id INT,
product_id INT,
created_at TIMESTAMP DEFAULT CURRENT_TIMESTAMP ON UPDATE CURRENT_TIMESTAMP,
PRIMARY KEY (cart_id)
) ;
Enable MySQL Event Scheduler
Start MySQL event scheduler by executing following query in PhpMyAdmin or MySQL command prompt.
SET GLOBAL event_scheduler = ON;
Or
SET GLOBAL event_scheduler = 1;
Or
SET GLOBAL event_scheduler = 1;
Create a Event
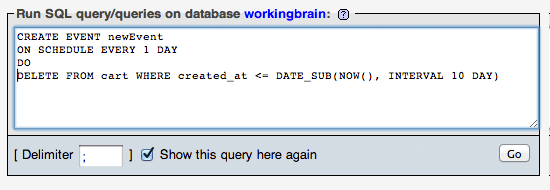
Here the following event will run everyday and clear/delete 10 days old data from cart table based on time stamp
CREATE EVENT newEvent
ON SCHEDULE EVERY 1 DAY
DO
DELETE FROM cart WHERE created_at <= DATE_SUB(NOW(), INTERVAL 10 DAY) ;
ON SCHEDULE EVERY 1 DAY
DO
DELETE FROM cart WHERE created_at <= DATE_SUB(NOW(), INTERVAL 10 DAY) ;
Alter Event
If you want to modify the event run time simple you can execute a query in below syntax.
ALTER newEvent
ON SCHEDULE EVERY 5 HOUR
STARTS TIMESTAMP + 3 HOUR
ON SCHEDULE EVERY 5 HOUR
STARTS TIMESTAMP + 3 HOUR
View Event
Show all the running events.
SHOW EVENTS;
Delete Event
You can drop the event for executing below query.
DROP EVENT newEvent;
Check event schedule status under process tab in PhpMyAdmin root (it will show only when scheduled event is running).
Thanks Arun, The tutorial is really informative as well as clear. I never had any idea that we can schedule an event in mySQL
this is rather good - I have been using Cron jobs to do the same thing .... now I don't think I will have to.
cool nice post thanks arun i'll search more about it.
Its like cronjob , cool bro, i just know about it from you :D
I didn't know an Event Scheduler existed in MySQL. Good article!
very good.
9lessons wins!!!!
Very Nice Sri..It certainly help me in deleting data log which is not required.
Thank You!
Regards,
Mukund Chaudhary
Nice !
Cool.... Please give demo for this.
Thanks.
Very very nice.I dont have any idea about this type of feature in mysql.
hi dear...thanks fro sharing this document with us...I am frequent user of your blog...I used your some example to develop some rich web applications....so thanks a lot...But in this document...I found one bug when we alter a event...You have mentioned....
ALTER newEvent
ON SCHEDULE EVERY 5 HOUR
STARTS TIMESTAMP + 3 HOUR
actually it should be...
ALTER EVENT newEvent
ON SCHEDULE EVERY 5 HOUR
STARTS TIMESTAMP + 3 HOUR
otherwise...MYSQL Engine gives error...
Thanks...
Nice!
Thanks for sharing.. :)
very nice...
Very Very nice post
Great... I never knew events were there in MySQL.. Good one... Thanks :)
interesting...thanks
it run automatically or manually ???
thank you.
wow very cool tip...
thanks
nice one
similar like cronjob i guess? nice post.
You make it look amazingly simple, thanks !
This will save me a lot of research/trial and error time !!
I will definitely click on all your adds ! ;)
thanks...it helps me lot.
Event runs automatically.
wow,it's very nice !!!!!!!!!!!
Great Post Srini....... :)
From Which Version of Mysql. Event scheduler was support.
Can anyone know this?
good post!, can we use single event to delete from multiple tables/ databases? if yes , how?
tnx...:)
I didn't know this :D
Thanks Srinivas
thanks, guys / really helpful
What if we use cpanel based crons instead of this mysql interval... what you prefer .. Srinivas?
nice post,
thx a lot Srinivas
Nice, thanks for this Arun! Great post.
thanks
many thanks
hi could you tell me
What if mysql instance is restarted .. are the events persistent.. or should i create them a fresh .. bharath
Hello,
Nice post. It will help to reduce cronjob which are used only for database updates. Now only thing which i would like to know is that if i want to set it as interval for 1 day but it should run at exactly 00:01 minute then what settings are needed ?
Thank you
Tejas Mehta
Very useful info for emerging developers....
Good..............
Good
Nice to see it. Please post some thing for store procedure like this one.
nice post.Very useful info
such a nice post! didnt really know about that function and really needed it! Thank you!
Nice article, thanks!
This is very nice. Nice to knw you can schedule events on Mysql WOW!
Nice one...very helpful
Good post...how will be the performance of database? since it will check the database every second to trigger the event.
Thanks for this post :)
Thid id Lovely
lovely
What is the performance of this feature in a busy transactional table with lots of data say 30million rows?
Hi,
Is it possible to give other conditions in where clause with date. for example.
CREATE EVENT newEvent
ON SCHEDULE EVERY 1 DAY
DO
DELETE FROM cart WHERE status = 0 AND created_at <= DATE_SUB(NOW(), INTERVAL 10 DAY) ;
thanks for this post. this code is very much use full.
very helpful. tyvm
Thanks
Very interseting. There is a big divide on this one, you have cleared up a lot of the myths. Thank you
nice post.. Thank you!
Is there anu way to run php function like this? I want to do it like a cron job.. If you can please let me know as soon as possible..
Thank you for sharing this post….This post is really useful to me because i have that much of interest about this post.Thank you.
Thank u
I want to backup my DB every Day..How to do?
Very Nice Sri..It certainly help me in deleting data log which is not required.
Thank You!
Regards,
Sudhir Chaudhary
Thanks, It worked in my local, but I unable to create event in my server database. can you tell me the reason.
very very helpful
thanks
very helpful thnks..
nice post.it's realy help me..